超巨大望遠鏡アイデア

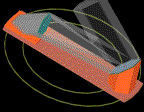
30m 望遠鏡 A案主鏡は放物面、リレー鏡は EL が独立に変動し、その結果、ビーム内での位相が階段状になる。構造としては安定するが、image size はかなり悪いことが予想される。PSF は評価中。スパイダーがないのが特徴。
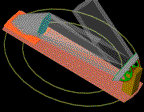30m 望遠鏡 B案これも主鏡は放物面だが、リレー鏡の架台は一体化しできる限り平面波の状態で主鏡に送る。主鏡を球面にして一種の反射型 Schmidt にできるかどうかは検討中。
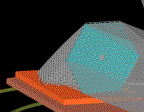主鏡(AB案共通)主鏡要素はとりあえず円形。鏡の隙間から風が逃げやすいのでは...
平面波に対する視野中心での理想的な PSF は下参照。放物面主鏡で補正レンズ無しの場合、視野中心から 20" でコマが 0.4" のサイズになる。巨大補正レンズを使えば 2' 位の視野は取れると思うが、ＳΩという意味ではすばる主焦点並にしての 8' 位欲しいところ。
主鏡要素(2mφ)一つの主鏡要素の口径は2m、周囲に焦点面を曲率中心とする位置制御用球面鏡を接着し、焦点面脇の波長可変レーザーと焦点面対角の位置に置かれた干渉計で全主鏡要素の位置を瞬時に計測する(できるかどうかはちゃんと考えていない)。
リレー鏡(A 案)全てのリレー鏡要素が独立に EL を変える。視野中心では、個々の主鏡要素に対し一つずつのリレー鏡が対応するが、巨大グレーティングのように働いて光路差を生じるため、結像精度はかなり悪そう。
リレー鏡要素
(A案 2m x 3m)		それぞれが EL 軸を持つ構造。技術的困難は殆んど無い。
リレー鏡(B 案)全体を巨大な架台に載せるため、制御が大変そう。技術的問題点としては、普通の経緯台式架台を作るのと大差ないかも。

以下、PSF の評価。分解能は 5cm で、計算した 4096x4096 pixel の中央 1/16 の部分について主鏡の復素透過率の実数部分(透過率 x cos(位相のずれ))と、各スケールでの PSF(波長1μm) を明るさの 10,100,10000倍で表したものを示す。

主鏡(30mφ)PSF(0.13"□,x10)PSF(1"□,x100)PSF(4"□,x10000)備考
各セグメントの位相のずれ無し。理想的な状態。
Peak: 1
各セグメントの位相のずれを 1σ=λ/8 の正規乱数で与えたもの。
即ち、セグメントの向きは変えずに光軸方向に 1σ=λ/16 のずれを与えた場合に相当。
Peak: 0.541276
位相のずれを 1σ=λ/4 の正規乱数で与えた場合(ほぼ A案に相当)。
Peak: 0.0852301
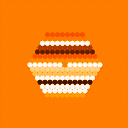縦方向の位相のずれを 1σ=λ/4 の正規乱数で与え、横方向の位相のずれが無い場合(A案で目指せるベスト)。
Peak: 0.225424

これらの計算で分かったこと

巨大望遠鏡に関する調査

iwamuro@kusastro.kyoto-u.ac.jp